All the tests were done on an Arch Linux x86_64 machine with an Intel(R) Core(TM) i7 CPU (1.90GHz).
Empirical likelihood computation
We show the performance of computing empirical likelihood with
el_mean(). We test the computation speed with simulated
data sets in two different settings: 1) the number of observations
increases with the number of parameters fixed, and 2) the number of
parameters increases with the number of observations fixed.
Increasing the number of observations
We fix the number of parameters at \(p =
10\), and simulate the parameter value and \(n \times p\) matrices using
rnorm(). In order to ensure convergence with a large \(n\), we set a large threshold value using
el_control().
library(ggplot2)
library(microbenchmark)
set.seed(3175775)
p <- 10
par <- rnorm(p, sd = 0.1)
ctrl <- el_control(th = 1e+10)
result <- microbenchmark(
n1e2 = el_mean(matrix(rnorm(100 * p), ncol = p), par = par, control = ctrl),
n1e3 = el_mean(matrix(rnorm(1000 * p), ncol = p), par = par, control = ctrl),
n1e4 = el_mean(matrix(rnorm(10000 * p), ncol = p), par = par, control = ctrl),
n1e5 = el_mean(matrix(rnorm(100000 * p), ncol = p), par = par, control = ctrl)
)Below are the results:
result
#> Unit: microseconds
#> expr min lq mean median uq max
#> n1e2 443.547 480.9065 518.9974 496.8265 548.883 825.529
#> n1e3 1168.178 1353.5780 2327.9855 1434.4295 1602.052 73838.491
#> n1e4 10433.479 12794.9310 14352.7309 14663.9095 15456.943 21782.395
#> n1e5 169461.720 223962.9690 265156.7597 252638.8225 316444.171 410333.021
#> neval cld
#> 100 a
#> 100 a
#> 100 b
#> 100 c
autoplot(result)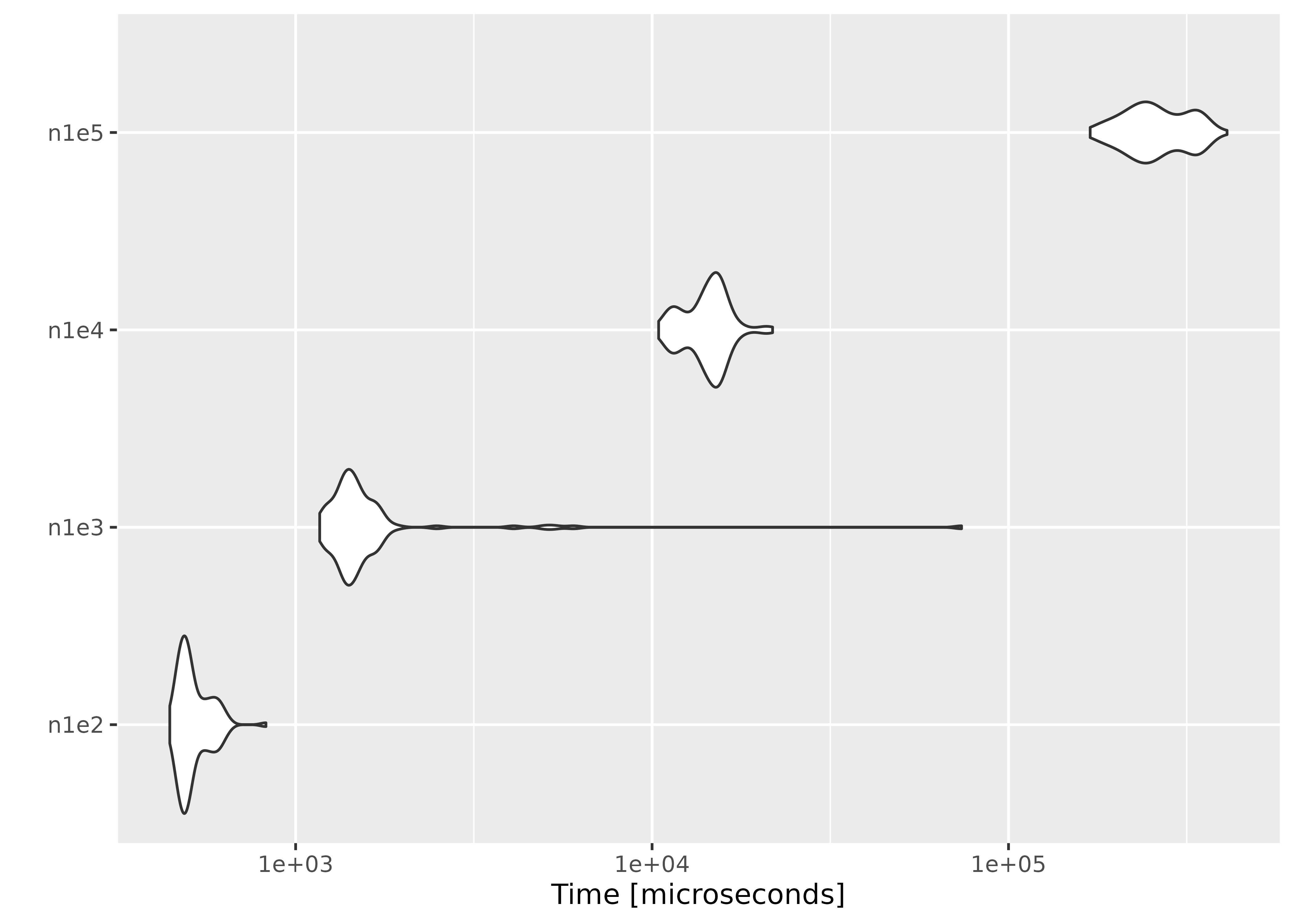
Increasing the number of parameters
This time we fix the number of observations at \(n = 1000\), and evaluate empirical likelihood at zero vectors of different sizes.
n <- 1000
result2 <- microbenchmark(
p5 = el_mean(matrix(rnorm(n * 5), ncol = 5),
par = rep(0, 5),
control = ctrl
),
p25 = el_mean(matrix(rnorm(n * 25), ncol = 25),
par = rep(0, 25),
control = ctrl
),
p100 = el_mean(matrix(rnorm(n * 100), ncol = 100),
par = rep(0, 100),
control = ctrl
),
p400 = el_mean(matrix(rnorm(n * 400), ncol = 400),
par = rep(0, 400),
control = ctrl
)
)
result2
#> Unit: microseconds
#> expr min lq mean median uq max
#> p5 715.554 767.4505 832.0326 791.751 829.6165 3910.269
#> p25 2715.402 2759.6440 2895.7267 2801.678 2860.2215 6707.533
#> p100 21704.880 24065.2350 26217.4337 25080.387 28799.2440 45835.691
#> p400 253630.477 278978.2515 312110.3298 298370.866 339284.6875 459820.159
#> neval cld
#> 100 a
#> 100 a
#> 100 b
#> 100 c
autoplot(result2)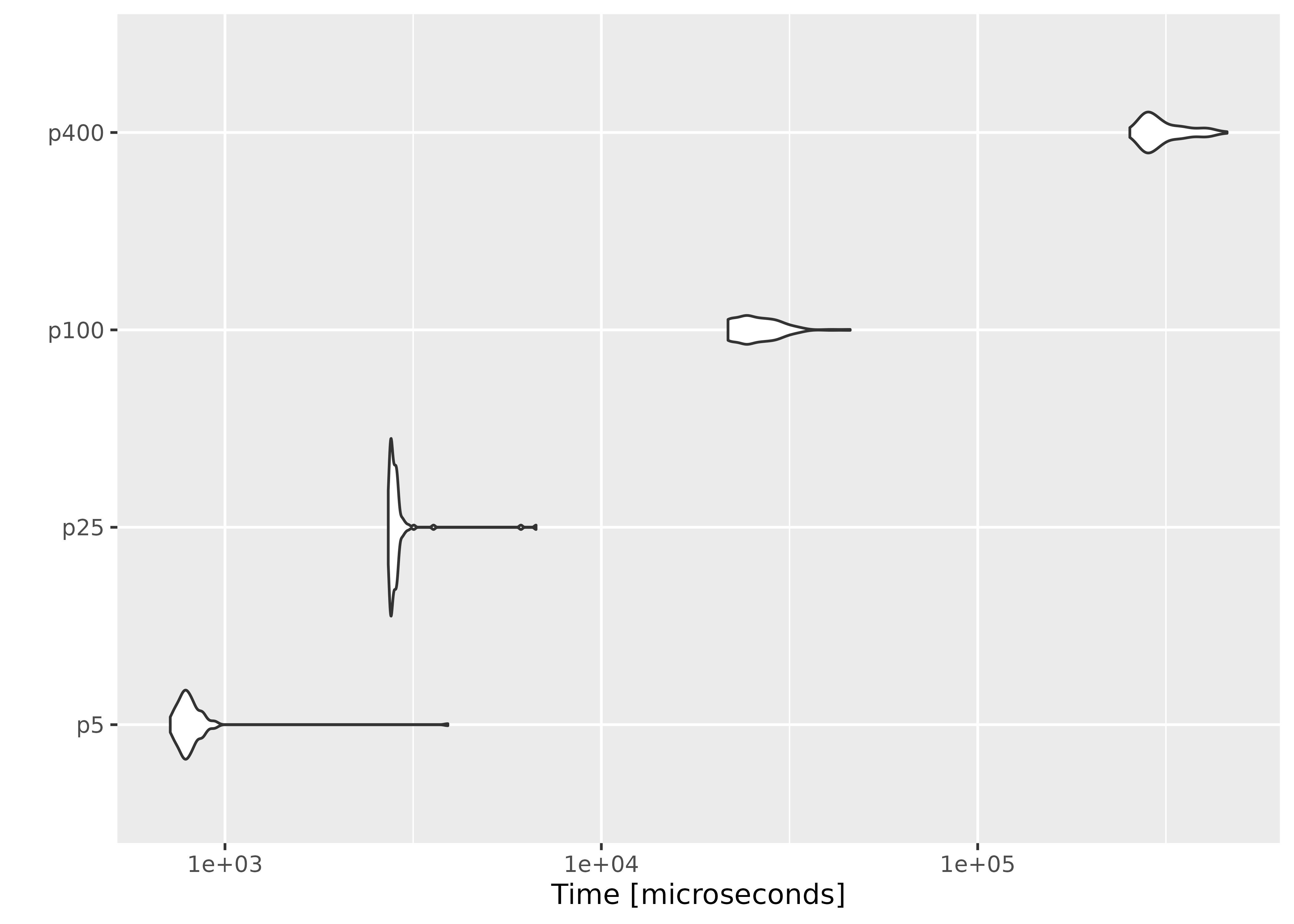
On average, evaluating empirical likelihood with a 100000×10 or 1000×400 matrix at a parameter value satisfying the convex hull constraint takes less than a second.