GLMMcosinor

Oliver Jayasinghe and Rex Parsons

An brief introduction to the cosinor model

A cosinor model aims to model the amplitude (\(A\)), acrophase (\(\phi\)), and MESOR (\(M\)) of a rhythmic dataset.

• MESOR (\(M\)) is the Midline Estimating Statistic of Rhythm, and may also be referred to as the equilibrium point.

• Amplitude (\(A\)) is the difference between the MESOR and the maximum height of the rhythm.

• Acrophase (\(\phi\)) is the phase at which the maximal response occurs.

These could be modelled using a cosine function:

\[Y(t) = M + Acos(\frac{2\pi t}{\tau} - \phi) + e(t)\] where \(e(t)\) is the error term.

However, these cannot be estimated using a linear modelling framework! Other packages, including {circacompare} (Parsons et al. 2020), fit this exact nonlinear model but most packages (including this one) decomposes this into linear terms, creating the cosinor model:

\[Y(t) = M + \beta x + \gamma z + e(t)\]

Where \(x =cos(\frac{2\pi t}{τ})\), \(z =sin(\frac{2\pi t}{τ})\), \(\beta = A cos(\phi)\), \(\gamma = A sin(\phi)\)

These original parameters can be recovered: for amplitude (\(A\)) and acrophase (\(\phi\)), the estimates for \(\hat\beta\) and \(\hat\gamma\) must be transformed as per the following equations:

\[\hat\phi = \arctan(\frac{\hat\gamma}{\hat\beta}) \]

\[\hat A = \sqrt{\hat\beta ^2 + \hat\gamma ^ 2}\] For a more thorough introduction to cosinor modelling, see here (Cornelissen 2014).

Introduction

GLMMcosinor allows the user to fit generalised linear models based on rhythmic data with a cosinor model. It allows users to summarise, predict, and plot these models too. Existing packages have focused primarily on Gaussian data. Some circadian regression modelling packages have allowed users to specify generalised linear models, but with limited flexibility. GLMMcosinor takes a comprehensive approach to modelling by harnessing the glmmTMB package, that has a wide range of available link functions, allowing users to model rhythmic data from a wide range of distributions (for full list - see ?family and ?glmmTMB::family_glmmTMB) including:

• Binomial
• Guassian
• Inverse Gaussian
• Gamma
• Poisson
• Negative Binomial

The table below shows what features are available within GLMMcosinor and other methods.

Software	Language	Multicomponent	Dispersion model	Zero-inflated model	Differential rhythmicity	Parameter estimates for differences	Family (available link functions)	Estimated parameters	Reference
GLMMcosinor	R	✓	✓	✓	✗	✓	n > 15 Any family avilable in {glmmTMB}: Gaussian, gamma, binomial, Poisson, …	Amplitude, acrophase, MESOR	Parsons, 2023
CircaCompare	R	✗	✗	✗	✗	✓	n = 1 Gaussian	Amplitude, acrophase, MESOR, and exponential decay of any of these characteristics or the differences in them between groups	Parsons, 2020
Cosinor	R	✗	✗	✗	✓	✓	n = 1 Gaussian	Amplitude, acrophase, MESOR	Sachs, 2014
Cosinor2	R	✗	✗	✗	✓	✓	n = 1 Gaussian	Amplitude, acrophase, MESOR	Mutak, 2018
CosinorPy	Python	✓	✗	✗	✓	✓	n = 3 Gaussian, Poisson, negative-binomial	Amplitude, acrophase, MESOR	Moskon, 2020
DiscoRhythm	R	✗	✗	✗	✗	✗	n = 1 Gaussian	Amplitude, acrophase	Carlucci, 2019
FMM	R	✓	✗	✗	✗	✓	n = 1 Gaussian	Amplitude, FMM phase angle parameters: alpha, beta, gamma	Fernández, 2022
Kronos	R	✓	✗	✗	✓	✓	n = 1 Gaussian	Amplitude, acrophase, MESOR	Bastiaanssen, 2023
LimoRhyde	R	✗	✗	✗	✓	✓	n = 1 Gaussian	Amplitude, acrophase, MESOR, period	Singer, 2019
RhythmCount	Python	✓	✗	✓	✗	✓	n = 6 Poisson, generalised-Poisson, zero-inflated Poisson, negative binomial, zero-inflated negative-binomial	Amplitude, acrophase, MESOR, Zenith	Velikajne, 2022

cglmm()

cglmm() wrangles the data appropriately to fit the cosinor model given the formula specified by the user. It returns a model, providing estimates of amplitude, acrophase, and MESOR (Midline Statistic Of Rhythm).

The formula argument for cglmm() is specified using the lme4 style (for details see vignette("lmer", package = "lme4")). The only difference is that it allows for use of amp_acro() within the formula that is used to identify the cosinor (rhythmic) components and relevant variables in the provided data. Any other combination of covariates can also be included in the formula as well as random effects. Additionally, zero-inflation (ziformula) and dispersion (dispformula) formulae can be incorporated if required. For detailed examples of how to specify these types of models, see the mixed-models, model-specification and multiple-components vignettes.

For example, consider the following model and its output:

library(GLMMcosinor)

cosinor_model <- cglmm(
  vit_d ~ X + amp_acro(time, period = 12, group = "X"), 
  data = vitamind
)

Notice how both the raw and transformed coefficients are provided as output. The adapted data.frame that was used to fit the raw model can be accessed from the model and includes main_rrr1 and main_sss1 columns of data:

head(cosinor_model$newdata)
#>      vit_d      time X  main_rrr1  main_sss1
#> 1 16.12091 11.439525 0  0.9572476 -0.2892699
#> 2 29.90624  5.807104 0 -0.9949038  0.1008285
#> 3 39.17572  1.045492 1  0.8538711  0.5204846
#> 4 35.15403  4.082983 1 -0.5371451  0.8434899
#> 5 43.67065 10.606247 1  0.7453295 -0.6666963
#> 6 31.20360  5.126054 0 -0.8971168  0.4417935

In this example, the main prefix indicates that this is the data for the conditional model, as opposed to (potential) dispersion or zero-inflation models, which have the prefixes disp and zi, respectively. The numeric suffix, indicates that this is the data for the first (and only) cosinor component. If there are multiple components, the columns of data will be named accordingly.

A basic overview of cglmm()

The cglmm() function is used to fit cosinor models to a variety of distributions using the glmmTMB() function.

cglmm(
  formula = vit_d ~ amp_acro(time, period = 12), 
  data = vitamind, 
  family = gaussian
)
#> 
#>  Conditional Model 
#> 
#>  Raw formula: 
#> vit_d ~ main_rrr1 + main_sss1 
#> 
#>  Raw Coefficients: 
#>             Estimate
#> (Intercept) 30.25467
#> main_rrr1    2.59418
#> main_sss1    5.75079
#> 
#>  Transformed Coefficients: 
#>             Estimate
#> (Intercept) 30.25467
#> amp          6.30883
#> acr          1.14703

• formula: A formula specifying the model structure, including the response variable and the cosinor components (using amp_acro()).
• data: The data.frame containing the variables used in the formula.
• family: The family of the distribution for the response variable (e.g., poisson, gaussian, or any family found in?family and ?glmmTMB::family_glmmTMB)

The amp_acro() function is used within the formula to specify the cosinor components. It allows you to specify the period of the rhythm and, if necessary, the grouping structure and the number of components. The arguments of amp_acro() are:

• group: The name of the grouping variable in the dataset.
• time_col: The name of the time column.
• n_components: The number of components in the cosinor model.
• period: The period(s) of the rhythm.

Understanding the output

The most relevant output from the cglmm() function is likely to be the parameter estimates for MESOR, amplitude, and acrophase under the ‘Transformed Coefficients’ heading. These are the recovered estimates mentioned at the beginning of this vignette: the amplitude and phase. The ‘Raw Coefficients’ are the coefficients from the cosinor model. In this example, the main_rrr1 and main_sss1 correspond to \(\hat\beta\) and \(\hat\gamma\) in the first section, respectively.

The following example fits a grouped single-component model with a Guassian distribution (the default).

cglmm(
  vit_d ~ X + amp_acro(time, period = 12, group = "X"), 
  data = vitamind
)
#> 
#>  Conditional Model 
#> 
#>  Raw formula: 
#> vit_d ~ X + X:main_rrr1 + X:main_sss1 
#> 
#>  Raw Coefficients: 
#>              Estimate
#> (Intercept)  29.68980
#> X1            1.90186
#> X0:main_rrr1  0.93079
#> X1:main_rrr1  6.51029
#> X0:main_sss1  6.20099
#> X1:main_sss1  4.81846
#> 
#>  Transformed Coefficients: 
#>             Estimate
#> (Intercept) 29.68980
#> [X=1]        1.90186
#> [X=0]:amp    6.27046
#> [X=1]:amp    8.09947
#> [X=0]:acr    1.42181
#> [X=1]:acr    0.63715

Under the ‘Transformed Coefficients’ heading:

• (Intercept) = 29.6898is the MESOR estimate of group 0

• [X=1] = 1.90186 is the difference between the MESOR estimates of group 1 and 2 *

• [X=0]:amp = 6.27046 is the amplitude estimate for group 0

• [X=1]:amp = 8.09947 is the amplitude estimate for group 1

• [X=0]:acr = 1.42181 is the acrophase estimate in radians for group 0 **

• [X=1]:acr = 0.63715 is the acrophase estimate in radians for group 1

* Hence, the MESOR estimate for group 1 would be 29.6898 + 1.90186 = 31.59166. This is due to the behaviour of the glmmTMB() function. This can be adjusted by adding a 0 + to the beginning of the formula:

cglmm(
  vit_d ~ 0 + X + amp_acro(time,
    period = 12,
    group = "X"
  ),
  data = vitamind
)
#> 
#>  Conditional Model 
#> 
#>  Raw formula: 
#> vit_d ~ X + X:main_rrr1 + X:main_sss1 - 1 
#> 
#>  Raw Coefficients: 
#>              Estimate
#> X0           29.68980
#> X1           31.59165
#> X0:main_rrr1  0.93079
#> X1:main_rrr1  6.51029
#> X0:main_sss1  6.20101
#> X1:main_sss1  4.81847
#> 
#>  Transformed Coefficients: 
#>           Estimate
#> [X=0]     29.68980
#> [X=1]     31.59165
#> [X=0]:amp  6.27048
#> [X=1]:amp  8.09948
#> [X=0]:acr  1.42181
#> [X=1]:acr  0.63716

Note how now, [X=1] = 31.59165 and this represents the estimate for the MESOR for group 1, rather than the difference.

** Note how the acrophase is provided in units of radians. Since the period is 12, an acrophase of 1.42181 radians corresponds to a time of \(\frac{1.42181}{2 \pi} \times 12 = 2.715457\). This means the maximum response occurs at 2.715 time units. We can check this visually using the autoplot() function, looking at the [X=0] level (red line)

cosinor_model <- cglmm(
  vit_d ~ 0 + X + amp_acro(time,
    period = 12,
    group = "X"
  ),
  data = vitamind
)
autoplot(cosinor_model, predict.ribbon = FALSE)

More advanced cglmm() model specification

The cglmm() function allows you to specify different types of cosinor models with or without grouping variables. The function can also generate dispersion models and zero-inflation models. For more detailed explanations and examples, see the model-specification article.

Additionally, the cglmm() function provides more advanced functionality for multi-component models, and detailed explanations can be found in the multiple-components article.

The cglmm() function also allows mixed model specification. See the mixed-models article for more details.

Using summary() and testing for differences between estimates

The summary() method for the outputs from cglmm() provides a more detailed summary of the model and its parameter estimates and uncertainty. It outputs the estimates, standard errors, confidence intervals, and p-values for both the raw model parameters and the transformed parameters. The summary statistics do not represent a comparison between any groups for the cosinor components - that is the role of the test_cosinor_components() and test_cosinor_levels() functions.

Here is an example of how to use summary() with some simulated data:

testdata_simple <- simulate_cosinor(
  1000,
  n_period = 2,
  mesor = 5,
  amp = 2,
  acro = 1,
  beta.mesor = 4,
  beta.amp = 1,
  beta.acro = 0.5,
  family = "poisson",
  period = 12,
  n_components = 1,
  beta.group = TRUE
)

object <- cglmm(
  Y ~ group + amp_acro(times, period = 12, group = "group"),
  data = testdata_simple, family = poisson()
)
summary(object)
#> 
#>  Conditional Model 
#> Raw model coefficients:
#>                      estimate standard.error     lower.CI upper.CI    p.value
#> (Intercept)       4.998454143    0.003463730  4.991665357  5.00524 < 2.22e-16
#> group1           -1.002150001    0.005937109 -1.013786521 -0.99051 < 2.22e-16
#> group0:main_rrr1  1.082281784    0.003347565  1.075720677  1.08884 < 2.22e-16
#> group1:main_rrr1  0.876651962    0.006198710  0.864502713  0.88880 < 2.22e-16
#> group0:main_sss1  1.682350718    0.003919418  1.674668800  1.69003 < 2.22e-16
#> group1:main_sss1  0.481951764    0.005936670  0.470316105  0.49359 < 2.22e-16
#>                     
#> (Intercept)      ***
#> group1           ***
#> group0:main_rrr1 ***
#> group1:main_rrr1 ***
#> group0:main_sss1 ***
#> group1:main_sss1 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Transformed coefficients:
#>                    estimate standard.error     lower.CI upper.CI    p.value    
#> (Intercept)     4.998454143    0.003463730  4.991665357  5.00524 < 2.22e-16 ***
#> [group=1]      -1.002150001    0.005937109 -1.013786521 -0.99051 < 2.22e-16 ***
#> [group=0]:amp1  2.000409408    0.004275553  1.992029478  2.00879 < 2.22e-16 ***
#> [group=1]:amp1  1.000398004    0.007530397  0.985638697  1.01516 < 2.22e-16 ***
#> [group=0]:acr1  0.999134804    0.002034131  0.995147980  1.00312 < 2.22e-16 ***
#> [group=1]:acr1  0.502662068    0.007562019  0.487840783  0.51748 < 2.22e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

If we wanted to test the difference between the amplitude estimate for component 1 between group 1 and group 2, we can use the test_cosinor_levels() function:

test_cosinor_levels(object, x_str = "group", param = "amp")
#> Test Details: 
#> Parameter being tested:
#> Amplitude
#> 
#> Comparison type:
#> levels
#> 
#> Grouping variable used for comparison between groups: group
#> Reference group: 0
#> Comparator group: 1
#> 
#> cglmm model only has a single component and to compare
#>           between groups.
#> 
#> 
#> 
#> Global test: 
#> Statistic: 
#> 23339.2
#> 
#> P-value: 
#> 0
#> 
#> 
#> Individual tests:
#> Statistic: 
#> -152.77
#> 
#> P-value: 
#> 0
#> 
#> Estimate and 95% confidence interval:
#> -1 (-1.01 to -0.99)

The estimate here is the estimate of the difference between the inputted values, along with its confidence interval. The real parameters for amp in the first component were 2 and 1 for groups 0 and 1 respectively, and so the difference is approximately -1.

Now, consider an example where the difference is not so clear.

testdata_poisson <- simulate_cosinor(100,
      n_period = 2,
      mesor = 7,
      amp = c(0.1, 0.5),
      acro = c(1, 1),
      beta.mesor = 4.4,
      beta.amp = c(0.1, 0.46),
      beta.acro = c(0.5, -1.5),
      family = "poisson",
      period = c(12, 6),
      n_components = 2,
      beta.group = TRUE
    )

cosinor_model <- cglmm(
  Y ~ group + amp_acro(times,
    period = c(12, 6),
    n_components = 2,
    group = "group"
  ),
  data = testdata_poisson,
  family = poisson()
)
test_cosinor_levels(
  cosinor_model, 
  x_str = "group", 
  param = "amp",
  component_index = 1
)
#> Test Details: 
#> Parameter being tested:
#> Amplitude
#> 
#> Comparison type:
#> levels
#> 
#> Grouping variable used for comparison between groups: group
#> Reference group: 0
#> Comparator group: 1
#> 
#> cglmm model has2 components. Component 1 is being used for comparison between groups.
#> 
#> 
#> 
#> Global test: 
#> Statistic: 
#> 0.05
#> 
#> P-value: 
#> 0.8223
#> 
#> 
#> Individual tests:
#> Statistic: 
#> -0.22
#> 
#> P-value: 
#> 0.8223
#> 
#> Estimate and 95% confidence interval:
#> 0 (-0.04 to 0.03)

In this example, there is no significant difference in the estimate of amp for the first component between the reference group and the comparator group. Also notice how if we are comparing between levels, we should keep the component the same, and that is what component_index sets. Likewise, when we test between components using test_cosinor_components(), we can indicate which level this comparison occurs using level_index. There may be multiple groups, in which case we can fix the group using the x_str argument.

As an example of testing the difference between components for the same level:

test_cosinor_components(
  cosinor_model, 
  x_str = "group",
  param = "acr",
  level_index = 1
)
#> Test Details: 
#> Parameter being tested:
#> Acrophase
#> 
#> Comparison type:
#> components
#> 
#> Component indices used for comparison between groups: group
#> Reference component: 1
#> Comparator component: 2
#> 
#> 
#> Global test: 
#> Statistic: 
#> 95.32
#> 
#> P-value: 
#> 0
#> 
#> 
#> Individual tests:
#> Statistic: 
#> -9.76
#> 
#> P-value: 
#> 0
#> 
#> Estimate and 95% confidence interval:
#> -1.89 (-2.27 to -1.51)

In this situation, there is a significant difference between the acrophase for the comparator group between its two components.

Using predict()

The predict() method allows users to get predicted values from the model on either the existing or new data.

cbind(predictions = predict(cosinor_model, type = "response"), testdata_poisson)

#>   predictions    Y     times group
#> 1    865.8332  871 17.009450     0
#> 2    701.2750  714 10.503837     0
#> 3    798.4445  861  4.800118     0
#> 4   1551.0482 1541 18.409584     0
#> 5   1733.9702 1699 12.315885     0
#> 6   1972.1517 1951  1.072893     0

Plotting cglmm objects

The GLMMcosinor package includes two ways to visualise cglmm() objects. Firstly, the autoplot() method creates a time-response plot of the fitted model for all groups:

autoplot(cosinor_model, superimpose.data = TRUE)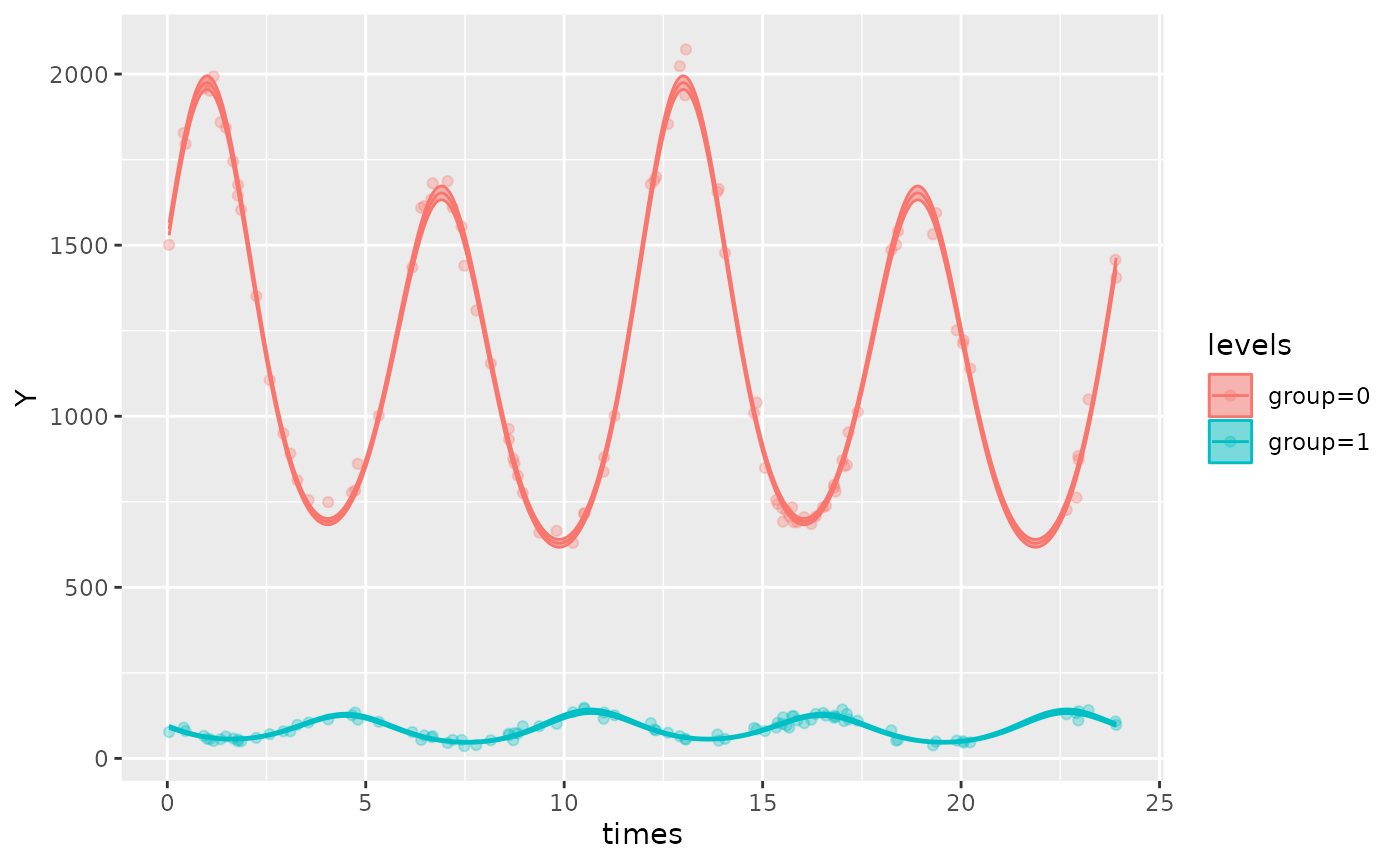

This function also allows users to superimpose the data (that was used to fit the model) over the fitted model, using the superimpose.data = TRUE, as demonstrated above. By default, the generated plot will have x-limits corresponding to the minimum and maximum values of the time-vector in the original dataframe, although the x-limits can be manually defined by the user using the xlims argument. The details of using the autoplot function are found in the model-visualisations vignette.

References

Cornelissen, Germaine. 2014. “Cosinor-Based Rhythmometry.” Theoretical Biology and Medical Modelling 11 (1): 1–24.

Parsons, Rex, Richard Parsons, Nicholas Garner, Henrik Oster, and Oliver Rawashdeh. 2020. “CircaCompare: A Method to Estimate and Statistically Support Differences in Mesor, Amplitude and Phase, Between Circadian Rhythms.” Bioinformatics 36 (4): 1208–12.